By Selena K. Chin, Grunde Jomaas, Peter B. Sunderland
Nozzle reaction is the force exerted by a fire nozzle on a firefighter. The NFPA reports there are an average 13,795 firefighting injuries annually associated with handling charged hose lines.
Nozzle reactions can limit a firefighter’s water application rate and increase his or her air consumption rate. Firefighters may incorrectly assume a high nozzle reaction implies a high water application rate.
A new paper published in Fire Technology, Firefighter nozzle reaction, explains nozzle reaction fluid mechanics for the first time. This is an interesting engineering problem that has defied a general solution for more than 100 years. This paper makes several simplifying assumptions. For example, it neglects hose stiffness, friction between the ground and the hose, gravity and fluid friction.
Nozzle reaction and hose tension are analyzed using fluid momentum conservation and assuming steady, inviscid flow and a flexible hose in frictionless contact with the ground.
An expression independent of the bend angle is derived for the hose tension. If this tension is exceeded owing to anchor forces, the hose becomes straight. The nozzle reaction is found to equal the jet momentum flow rate, and it does not change when an elbow connects the hose to the nozzle.
A forward force must be exerted by a firefighter or another anchor that matches the forward force that the jet would exert on a perpendicular wall.
Nozzle reaction expressions
Three reaction expressions are derived, allowing it to be determined in terms of hose diameter, jet diameter, flowrate and static pressure upstream of the nozzle. The nozzle reaction predictions used by the fire service are 56 percent to 90 percent of those obtained here for typical firefighting hand lines.
Sharing these findings with the fire protection community can improve firefighter safety.
The nozzle reaction is found to be:
R = ρ Q 2 / A2 ,
where A2 is the discharge diameter, Q is the volumetric flow rate, R is the magnitude of the nozzle reaction, and r is the water density. This equation shows that the reaction is proportional to the flow rate squared, divided by the nozzle diameter.
This equation is plotted in Fig. 1. Three different curves are shown, for different nozzle diameters (d2). The plot and equation show that nozzle reaction increases with flow rate squared. The vertical lines in Fig. 1 are the NFPA requirements for the initial attack line and the backup line. NFPA 1964, Standard for Spray Nozzles, provides performance requirements for firefighting spray nozzles suitable for fire suppression use. The horizontal line is the maximum reaction that a typical firefighter can handle alone. This limit can easily be surpassed with a high flow rate and/or a small nozzle diameter.
If Q is unknown, find the reaction from:
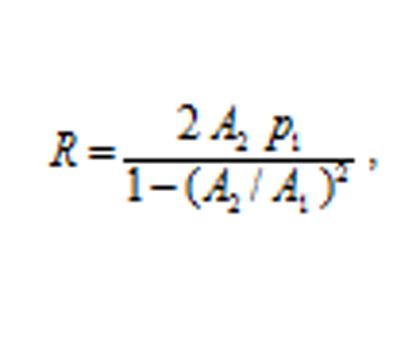
where A1 and p1 are the hose area and the nozzle’s gauge static pressure.
If A2 is unknown, find the reaction from:
R = ( 2 ρ Q2 p1 + ρ2 Q4 / A12 ) 0.5 .
This equation shows that for a fully open bale valve and a hose area much larger than the nozzle area, the reaction is proportional to the flow rate times the square root of pressure.
Flow rate, pressure, hose area and jet area
The paper shows the same nozzle reaction occurs no matter how bent or straight the hose is. This conclusion contradicts some advice, published recently, that firefighters should try to hold their hose end straight.
Provided equations estimate nozzle reaction from sufficient flow rate, pressure, hose area and jet area knowledge.
The nozzle reaction equations published by the NFPA are reasonably accurate when the hose area is much larger than the smallest part of the nozzle. However, otherwise these lead to large underpredictions.
Unfortunately, the authors were unable to find any well documented measurements with which to test the new predictions. Any readers aware of such measurements are encouraged to please contact Peter Sunderland at the University of Maryland.
One limitation of the work is that hose stiffness and ground friction are neglected. Firefighters kneeling or sitting on the fire hose while spraying, is an effective strategy to reduce nozzle reaction tremendously.
In summary, here are the three key facts every firefighter needs to know about nozzle reaction:
- Holding the fire hose end straight will not reduce the nozzle reaction.
- The nozzle reaction is the same as the force the hose stream exerts on a vertical wall.
- With the bale valve fully open, nozzle reaction is proportional to flow rate times the square root of pressure.
About the authors
Selena Chin is an M.S. student in the Department of Fire Protection Engineering at the University of Maryland.
Grunde Jomaas is BRE chair of fire safety engineering at the University of Edinburgh.
Peter Sunderland is professor of fire protection engineering at the University of Maryland.













